|
УДК 630*5: 519.2 И.Н. Павлов, С.В. Ушанов
Исследование распределения деревьев сосны по диаметру Методами анализа смесей распределений
Рассматривается методика анализа смесей распределений в сложных системах. Представлены результаты исследования распределения деревьев сосны обыкновенной по диаметру в очагах интенсивного биогенного воздействия.
Введение. Для описания случайных величин в прикладных исследованиях используется около 30 законов и семейств распределения (Лемешко, 1998). Очевидно, что они не покрывают существующего многообразия распределения случайных величин.
Сложные биологические, технические, социальные системы включают совокупности элементов, принадлежащих, как правило, нескольким классам. Примером такой совокурности является система, состоящая из нормально функционирующих (1-й класс) и ослабленных (2-й класс) объектов (элементов). Достаточно распространена ситуация, когда априори неизвестно, какому классу принадлежит наблюдаемый элемент системы. Каждый класс объектов можно охарактеризовать некоторой функцией плотности распределения, описывающей закон распределения анализируемого признака. Распределение в такой системе может быть унимодальным, бимодальным и полимодальным. Модели смесей распределений являются достаточно адекватным математическим формализмом для описания эмпирических функций распределения анализируемого признака.
В нижнем течении р. Караульной (ООПТ зеленая зона г. Красноярска) на прилегающих сопках в последнее десятилетие наблюдается интенсивная куртинная гибель сосны обыкновенной. Усыханию подвержены деревья всех классов Крафта. Погибают экземпляры, не испытывающие каких-либо признаков угнетения, с хорошо развитой кроной. Гибель наступает очень быстро. Образуются очаги диаметром 10-30 м, в дальнейшем сливающиеся в полосы. Часто наблюдается гибель деревьев по периметру существующих окон в древостое. Куртинное усыхание, наличие плодовых тел Armillaria mellea sensu lato, а также ряд других диагностических признаков (Павлов, Миронов, 2004) свидетельствуют об интенсивном развитии армиллариоза. Изучение изменения в строении древостоев в условиях интенсивного биогенного воздействия представляет как теоретический, так и практический интерес.
Экспериментальная часть.
Для изучения кольцевых процессов распространения агрессивных видов грибных патогенов на полигоне 10,8 га было заложено 13 круговых ППП общей площадью 1,17 га. Использование круговых постоянных пробных площадей с картированием из центра через измеряемые угол и расстояние (Павлов, 2005) имеет значительные преимущества в сравнении с методами, предполагающими разбивку исследуемой территории регулярной сеткой. При значительном снижении трудоемкости сохраняется высокая точность определения координат. Исследуемый древостой сосны обыкновенной (9С1Ос +Б ед. Лц,) 5 класса возраста имеет полноту 1,0 (2 бонитет).
В связи с тем, что усыхание на изученных ППП произошло за достаточно короткий период времени под влиянием экстремального фактора, представляет особый интерес знание о предшествующем воздействию строении древостоя. Эмпирическая функция распределения древостоев сосны обыкновенной по диаметру (представлены все деревья, растущие в настоящее время и усохшие в последнее десятилетие) в очагах интенсивного биогенного повреждения грибами комплекса Armillaria mellea sensu lato является бимодальной (рис. 1) и может быть описана смесью не менее двух распределений. Общий объем выборочных данных равен 743. Анализ параметров и доли наблюдений, приходящихся на каждую составляющую смеси, проводится статистическими методами.
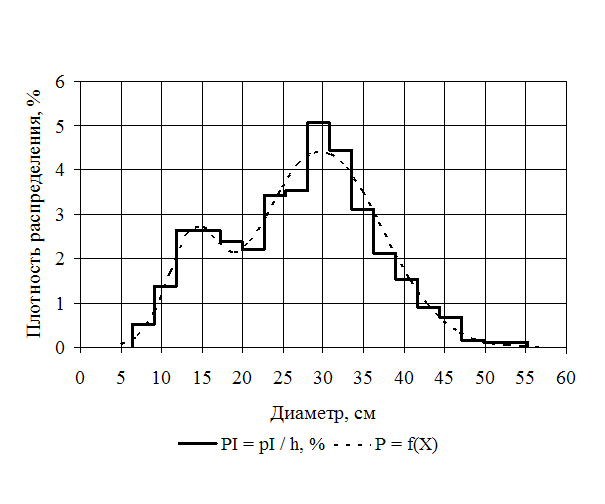
Рис. 1 – Функции плотности распределения древостоя сосны обыкновенной, нарушенного грибами комплекса Armillaria mellea sensu lato
Методика и основные задачи исследования.
Впервые алгоритм разделения совокупности на две нормальные составляющие методом моментов предложил К. Пирсон. В дальнейшем метод был упрощен, появились работы по разделению смеси биноминальных распределений, Пуассона, Вейбулла (Никитин, Швиденко, 1978).
Уравнение функции плотности смеси вероятностных распределений f(x), описывающее закон распределения анализируемого признака во всей (объединенной) генеральной совокупности имеет вид:
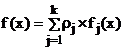 , (1) , (1)
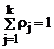 , rj ? 0, , rj ? 0, 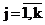 , (2) , (2)
где rj – удельный вес (доля) j - го компонента смеси (априорные вероятности появления наблюдений из j - го класса объектов), fj(x) = jj(aj,x) - плотность распределения анализируемого признака для j- го класса, aj – векторные параметры, от значений которых зависит закон распределения j- го компонента смеси, 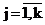 - номер класса, k – число классов. - номер класса, k – число классов.
При анализе распределения выборочных данных рассматриваемых систем решаются четыре основные задачи.
Первая задача (задача 1) – это задача параметрической идентификации функции плотности смеси вероятностных распределений (1). Это задача нелинейного программирования, при решении которой определяются параметры rj, aj 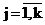 функции (1), которые минимизируют расчетное значение одного из статистических критериев согласия Колмогорова (Dрас), Лемана – Розенблатта (w2рас), Пирсона (c2рас) (Феллер, 1984; Айвазян, Мхитарян, 2001; Орлов, 2002; Ушанов, 2003) или обобщенного критерия функции (1), которые минимизируют расчетное значение одного из статистических критериев согласия Колмогорова (Dрас), Лемана – Розенблатта (w2рас), Пирсона (c2рас) (Феллер, 1984; Айвазян, Мхитарян, 2001; Орлов, 2002; Ушанов, 2003) или обобщенного критерия
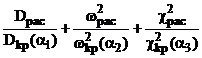 (3) (3)
при условиях (2) и некоторых дополнительных ограничениях на изменение параметров aj 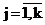 . В выражении (3) Dkp(a1), w2kp(a2), c2kp(a3) – критические значения критериев согласия Колмогорова, Лемана – Розенблатта и Пирсона при уровнях значимости a1, a2, a3. Опыт практического решения задачи 1 показал, что она достаточно эффективно решается квазиньютоновскими методами второго порядка (Рубан, 2001) с использованием стандартных инструментальных средств систем Excel и MathCad. . В выражении (3) Dkp(a1), w2kp(a2), c2kp(a3) – критические значения критериев согласия Колмогорова, Лемана – Розенблатта и Пирсона при уровнях значимости a1, a2, a3. Опыт практического решения задачи 1 показал, что она достаточно эффективно решается квазиньютоновскими методами второго порядка (Рубан, 2001) с использованием стандартных инструментальных средств систем Excel и MathCad.
Вторая из решаемых задач (задача 2) заключается в построении доверительных областей изменения параметров функции (1) (Ушанов, 2003; Соколов, Гладких, 2004). Решение этой задачи нелинейного программирования позволяет оценить границы изменения коэффициентов rj, aj, 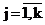 . Надежность выделения j – го класса в смеси оценивается значимостью отличия от нуля коэффициентов rj, . Надежность выделения j – го класса в смеси оценивается значимостью отличия от нуля коэффициентов rj, 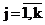 . Решение задачи 2 позволяет более обоснованно подойти к оценке влияния внешних факторов на изменения параметров функций плотностей распределений. . Решение задачи 2 позволяет более обоснованно подойти к оценке влияния внешних факторов на изменения параметров функций плотностей распределений.
Третья задача (задача 3) – это задача расщепления смеси распределений (Айвазян, Мхитарян, 2001; Орлов, 2002). Цель решения этой задачи заключается в статистической оценке числа компонентов смеси, их удельных весов (априорных вероятностей) rj, 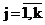 и функций плотностей распределений fj(x), и функций плотностей распределений fj(x), 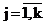 . При решении задачи 3 для каждого из альтернативных законов распределения решаются задачи 1 - 2. Гипотеза согласованности выборочной и расчетной функций распределения не отвергается, если расчетное значение критерия согласия не превосходит критического значения при заданном уровне значимости. Из дальнейшего анализа исключаются распределения, для которых не принимается гипотеза согласованности выборочной и расчетной функции распределения. Оставшиеся распределения упорядочиваются по уменьшению расчетного значения критерия согласия. Надежность выделения классов оценивается решением задачи 2. При отсутствии априорных сведений о числе компонентов смеси k и законах распределения fj(x), . При решении задачи 3 для каждого из альтернативных законов распределения решаются задачи 1 - 2. Гипотеза согласованности выборочной и расчетной функций распределения не отвергается, если расчетное значение критерия согласия не превосходит критического значения при заданном уровне значимости. Из дальнейшего анализа исключаются распределения, для которых не принимается гипотеза согласованности выборочной и расчетной функции распределения. Оставшиеся распределения упорядочиваются по уменьшению расчетного значения критерия согласия. Надежность выделения классов оценивается решением задачи 2. При отсутствии априорных сведений о числе компонентов смеси k и законах распределения fj(x), 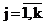 , задача расщепления смеси распределений, как правило, не имеет однозначного решения. Как и в задаче построения регрессионных уравнений при прочих равных условиях предпочтение отдается альтернативным решениям с минимальным числом компонентов смеси и характерными для рассматриваемых систем функциями плотности распределения. , задача расщепления смеси распределений, как правило, не имеет однозначного решения. Как и в задаче построения регрессионных уравнений при прочих равных условиях предпочтение отдается альтернативным решениям с минимальным числом компонентов смеси и характерными для рассматриваемых систем функциями плотности распределения.
Четвертая задача – задача автоматической классификации (Ушанов, 2003; Соколов, Гладких, 2004). В рамках модели смеси распределений наблюдение следует отнести к тому классу j0, в рамках которого оно выглядит наиболее правдоподобно:
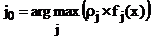 . (4) . (4)
Для некоторого наблюдения х вероятность Pj(х) отнесения объекта к j – му классу определяется выражением
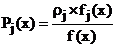 , , 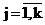 . (5) . (5)
Результаты.
Эмпирическая функция плотности распределения древостоя сосны обыкновенной, поврежденного грибами комплекса Armillaria mellea sensu lato аппроксимировалась одно, двух и трех компонентной смесью нормальных распределений:
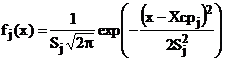 , , 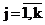 , (6) , (6)
где Xсрj , Sj2 – оценки математического ожидания и дисперсии j – й компоненты к компонентной функции плотности смеси нормальных распределений древостой сосны обыкновенной по диаметру х.
Параметры распределений определялись решением задачи 1 минимизацией обобщенного критерия (3). Результаты решения задачи 1 параметрической идентификации функций плотности одно-, двух- и трехкомпонентной смеси нормальных распределений представлены в табл. 1. В табл. 2 представлены результаты проверки согласованности эмпирической и теоретических функций смесей распределений по критериям согласия Колмогорова (D), Лемана – Розенблатта (w2), Пирсона (c2). Учитывая рекомендации (Орлов, 2002; Справочник по …, 1989, 1990) проверку согласованности функций распределения проводили при уровнях значимости a1 = 0,2 – для критерия Колмогорова, a2 = 0,5 – для критерия Лемана – Розенблатта, a3 = 0,05 – для критерия Пирсона.
Таблица 1
Оптимальные значения параметров смеси одно-, двух- и трехкомпонентных смесей нормальных распределений древостоя сосны обыкновенной, поврежденного грибами комплекса Armillaria mellea sensu lato
Число компонентов смеси |
Первая компонента |
Вторая компонента |
Третья компонента |
Xср1 |
S1 |
r1 |
Xср2 |
S2 |
r2 |
Xср3 |
S3 |
r3 |
1 |
27,0 |
9,4 |
1,000 |
|
|
|
|
|
|
2 |
29,7 |
7,5 |
0,826 |
13,8 |
3,1 |
0,174 |
|
|
|
3 |
29,0 |
8,4 |
0,797 |
13,8 |
2,8 |
0,143 |
30,8 |
2,0 |
0,070 |
Таблица 2
Результаты согласованности эмпирических и расчетных функций распределения по критериям согласия Колмогорова (D), Лемана – Розенблатта (w2), Пирсона (c2)
Проверка гипотезы о соответствии функции распределения выборочных данных с функциями смесей нормальных распределений |
Критерий
согласия |
Показатели |
Число компонентов смеси |
1 |
2 |
3 |
Колмогорова
(D) |
Dрас |
0,046 |
0,013 |
0,013 |
a |
0,200 |
0,200 |
0,200 |
Dkp(a) |
0,041 |
0,041 |
0,041 |
Вывод: гипотеза |
отклоняется |
не отклоняется |
Лемана-Розенблатта (w2) |
(Nw2)рас |
0,36 |
0,04 |
0,02 |
a |
0,500 |
0,500 |
0,500 |
(Nw2)кр |
0,12 |
0,12 |
0,12 |
Вывод: гипотеза |
отклоняется |
не отклоняется |
Пирсона (c2) |
cpac2 |
55,3 |
12,5 |
4,4 |
число параметров, с |
2 |
8 |
8 |
Число степеней свободы |
15 |
9 |
9 |
a |
0,050 |
0,050 |
0,050 |
ckp2 |
25,0 |
21,0 |
16,9 |
Вывод: гипотеза |
отклоняется |
не отклоняется |
Решение задачи 3 показало, что удельный вес третьей компоненты r3 трехкомпонентной смеси нормальных распределений не существенно отличается от нуля, а функция распределения двухкомпонентной смеси статистически незначимо отличается от функции распределения выборочных данных (табл. 2). Соответствующие функции распределений и функции плотностей распределений представлены на рисунках 1 и 2. Только использование двухнормального распределения позволило получить удовлетворительные значения по трем критериям согласия. Трехпараметрическая функция Вейбулла может быть принята только по критерию Колмогорова.
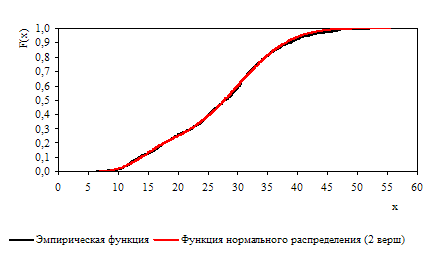
D=0,013; ?2=0,040
|
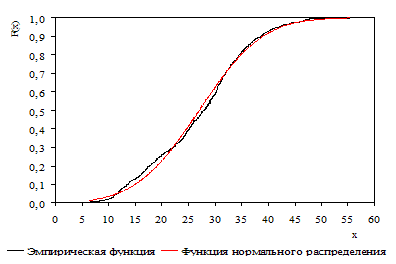
D= 0,0456; ?2=0,363
|
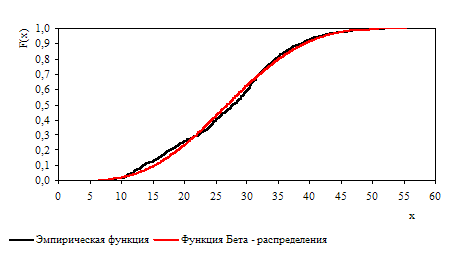
D= 0,0458; ?2=0,436
|
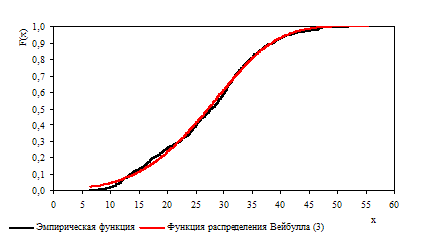
D=0,0344; ?2=0,189
|
Рис. Интегральная функция распределения (критерии согласия: D - Колмогорова, ?2 - Лемана-Розенблата)
Доверительные интервалы изменения параметров двухкомпонентной смеси нормальных распределений в области выполнения всех трех критериев согласия (Колмогорова, Лемана - Розенблатта, Пирсона) при указанных выше уровнях значимости определены решением задачи 2. Результаты расчетов приведены в табл. 3.
Таблица 3
Доверительные интервалы изменения параметров двухкомпонентной смеси нормальных распределений в области выполнения критериев согласия Колмогорова, Лемана - Розенблатта, Пирсона
Значения |
Параметры распределения |
Параметры
распределения |
Xср2 |
S2 |
Xср1 |
S1 |
r1 |
r2 |
Оптимум |
13,32 |
3,56 |
29,78 |
7,40 |
0,774 |
0,226 |
Минимум |
11,82 |
2,99 |
28,56 |
8,41 |
0,888 |
0,157 |
Xср2 I
[11,82 15,13] |
Максимум |
15,13 |
4,66 |
30,70 |
7,14 |
0,761 |
0,294 |
Минимум |
12,55 |
2,21 |
28,36 |
8,72 |
0,906 |
0,137 |
S2 I
[2,21 5,04] |
Максимум |
14,55 |
5,04 |
30,52 |
7,43 |
0,772 |
0,280 |
Минимум |
12,05 |
2,44 |
28,21 |
8,67 |
0,912 |
0,128 |
Xср1 I
[28,2 31,0] |
Максимум |
14,88 |
4,58 |
30,96 |
6,99 |
0,746 |
0,304 |
Минимум |
14,21 |
4,04 |
30,85 |
6,78 |
0,768 |
0,282 |
S1 I
[6,78 8,79] |
Максимум |
12,05 |
2,46 |
28,25 |
8,79 |
0,910 |
0,128 |
Минимум |
12,51 |
1,81 |
28,41 |
8,56 |
0,741 |
0,082 |
r1 I
[0,741 0,918] |
Максимум |
15,38 |
4,22 |
30,84 |
6,98 |
0,918 |
0,259 |
Минимум |
12,07 |
2,46 |
28,25 |
8,71 |
0,918 |
0,125 |
r2 I
[0,125 0,310] |
Максимум |
14,81 |
4,62 |
30,95 |
6,95 |
0,741 |
0,310 |
Первая компонента двухкомпонентной смеси распределений соответствует здоровым деревьям. Оценка математического ожидания этой компоненты равна 29,8 см, а интервальная оценка изменяется от 28,2 до 31,0 см. Оценка среднего квадратического отклонения первой компоненты равна 7,4 см, а интервальная оценка его изменяется от 6,8 до 8,8 см.
Вторая компонента двухкомпонентной смеси распределений соответствует больным и усохшим деревьям. Оценка математического ожидания этой компоненты равна 13,3 см, а интервальная оценка изменяется от 11,8 до 15,1 см. Оценка среднего квадратического отклонения второй компоненты равна 3,6 см, а интервальная оценка изменяется от 2,2 до 5,0 см.
Оценка удельного веса здоровых деревьев в генеральной совокупности равна 77,4 % (интервальная оценка изменяется от 74,1 % до 91,8 %). Оценка удельного веса ослабленных и усохших деревьев равна 22,6 % (интервальная оценка - от 12,5 % до 31,0 %). Эмпирической выборке объемом 743 деревьев соответствует 575 (от 551 до 682) неповрежденных деревьев и 168 (от 92 до 230) поврежденных и усохших деревьев.
Распределение числа здоровых, поврежденных и общего количества деревьев в зависимости от диаметра в выборке объема 743 представлена на рис. 3.
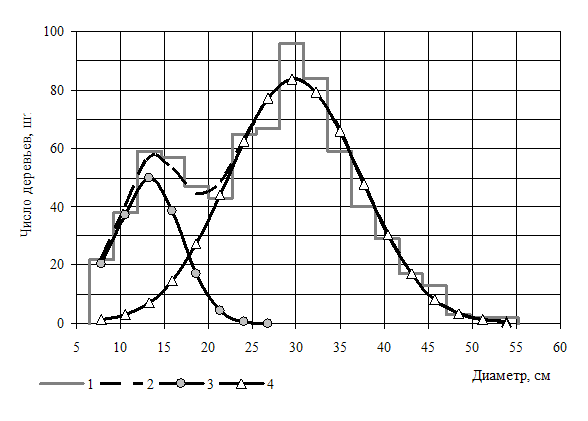
Рис. 3 – Распределение числа деревьев по диаметру (1, 2 – общее число; 3- ослабленные и усохшие; 4 – здоровые)
Предлагаемая методика анализа смесей распределений достаточно эффективна для изучения строения разновозрастных, смешанных или испытывающих значительное антропогенное и (или) биогенное воздействие насаждений.
Литература
- Айвазян С.А., Мхитарян В.С. Теория вероятностей и прикладная статистика. – М.: ЮНИТИ-ДАНА, 2001. – 656 с.
- Лемешко Б.Ю. Асимптотически оптимальное группирование наблюдений в критериях согласия //Заводская лаборатория, 1998. Т. 64. - №1. - С.56-64.
- Никитин К.Е., Швиденко А.З. Методы и техника обработки лесоводственной информации. М.: Лесн. пром-ть, 1972. -272 с.
- Орлов А.И. Эконометрика. – М.: Экзамен, 2002. – 576 с.
- Павлов И.Н. К методике картографирования куртинного усыхания деревьев с применением геоинформационных технологий // Лесное хозяйство – 2005. - № 4 – С.38-39.
- Павлов И.Н., Миронов А.Г. Куртинное усыхание хвойных насаждений в измененных условиях среды (вопросы диагностики) //Непрерывное экологическое образование и экологические проблемы: Сборник статей по материалам Всероссийской научно – практической конференции. Т.1. Красноярск: СибГТУ, 2004. С. 173-185.
- Рубан А.И. Методы оптимизации. – Красноярск: НИИ ИПУ, 2001. – 528 с.
- Соколов Г.А., Гладких И.М. Математическая статистика.- М.: Экзамен, 2004. – 432 с.
- Справочник по прикладной статистики. В 2-х т. Т.1: Пер. с англ./Под ред. Э. Ллойда, У. Ледермана, Ю.Н. Тюрина. – М.: Финансы и статистика, 1989, - 510 с.
- Справочник по прикладной статистики. В 2-х т. Т.2: Пер. с англ./Под ред. Э. Ллойда, У. Ледермана, С.А. Айвазяна, Ю.Н. Тюрина. – М.: Финансы и статистика, 1990, - 526 с.
- Ушанов С.В. Применение многомерных статистических методов при принятии решений. – Красноярск: СибГТУ, 2003. – 239 с.
- Феллер В. Введение в теорию вероятностей и ее приложения. В 2-х т. – Т.1 - М.: Мир, 1984, - 528 с. Т.2. – М.: Мир, 1984. – 738 с.
|




